В Интернете я нашел коллекцию определений (кто-то этим тоже заинтересовался), из которой видна наша полная беспомощность. Процитируем лучшие варианты.

• Процесс — изменение свойств некоторого объекта (при взаимодействии с другими элементами системы или внешней средой) или его перемещение в пространстве-времени (в нашем случае — предмета труда в материальной, информационной или финансовой форме), как реализация одной из целей системы. Например, изменение экономических характеристик товара при его хранении на складе.
   www.loza.spb.ru
• Процесс (от лат. processus — продвижение) — последовательная смена состояний объекта во времени. Природа объекта может быть произвольной: материальный (природный или искусственный) или идеальный (понятие, теория и т.п.) объект порождает соответственно материальный или идеальный процесс (например, процесс приготовления пищи, процесс любовных переживаний).
   ru.wikipedia.org/wiki/Процесс

Из этих определений видно, что процессом называется объект произвольной природы, который может находиться в различных состояниях и с течением времени переходить из одного состояния в другое. Сами эти переходы также называются процессом.

Мы рассмотрим простейшие процессы, встречающиеся в информатике, теории вероятностей и в задачах оптимизации.

Автоматом мы назовем пятерку  <S,A,B,T,s₀>,  где

• S, — непустое конечное множество, элементы которого называются состояниями автомата.
• A, — непустое конечное множество, называемое входным алфавитом автомата, его элементы называются буквами.
• B, — непустое конечное множество, называемое выходным алфавитом автомата, его элементы также называются буквами.
• T, — отображение  T: S × A →S × B .
• s₀, — начальное состояние автомата.

Автомат переходит из состояния в состояние под воздействием последовательности букв входного алфавита. Вначале он находится, как легко понять, в состоянии  s₀.  Поступает (говорят, на вход автомата) начальный элемент входной последовательности  a₁,  и отображение переводит пару  (s₀,a₁)  в пару  (s₁,b₁). Элемент  s₁  становится новым состоянием процесса, а элемент  b₁,  входит в выходную последовательность. Такие образом автомат переводит некоторую входную последовательность в выходную..

Получилась конструкция слишком простая и слишком общая. Рассмотрим простой пример.

Пусть исходная строка такова
когда_кончится_покос_соберем_и_кококос.
В нашем модифицированном алфавите на вход автомата поступит строка
ко----ко----с---окос-со--------кококос-
Вот какими будут состояния автомата после прочтения каждой очередной буквы (вначале 0)
120000120000000001200000000000012343450

Переходы из состояния в состояние можно описать графом переходов автомата, вершинами которого будут состояния автомата, а дугами — возможные переходы каждого такта работы.

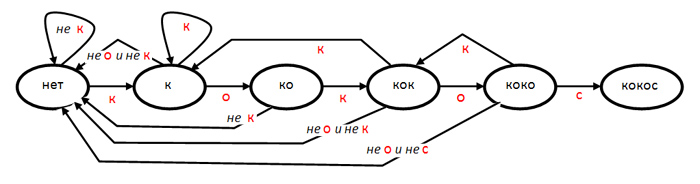
Вы видите шесть упомянутые состояний. Дуг, выходящих из последнего состояния, нет, мы считаем, что поиск завершается при обнаружении образца, и также при исчерпании строки ввода.

Трудоемкость такого поиска при использовании автомата составляется из двух частей — изготовления самого автомата, предназначенного для данного образца, и просмотра строки. Вторая часть имеет, очевидно, линейную трудоемкость (по длине строки). Оценкой трудоемкости первой части мы с вами заниматься не будем, но в лучших вариантах она линейна по длине образца.

Отметим еще, что в небольших автоматах удобно представлять отображение  T  в виде матрицы  T[S,A],  элементами которой должны быть пары из нового состояния автомата и выходного значения. В нашем примере эта таблица выглядит так (поразительно просто!)

Я не включил в таблицу последнее состояние и принимаемые решения, поскольку результатом является сам приход автомата в последнее состояние.

Например, если термин использован на страницах
16 23 24 31 37 38 39 41 42 54 55 56 57 58 59
то перечень в указателе должен выглядеть так
16, 23, 24, 31, 37-39, 41, 42, 54-59.
Перевод исходного перечня в этот стандартный формат удобно выполнять автоматом, который мы сейчас и разработаем.

Поступающие на обработку номера страниц мы переведем в символы входного алфавита. Их будет три: Н для начала группы в нумерации, П для продолжения, К для конца списка. В этом алфавите входная строка автомата будет для нашего примера такой
ННПННППНПНПППК
У этого автомата получается четыре состояния, которые мы перенумеруем от 0 до 3 и девять возможных действий, их перенимеруем от 0 до 8. Таким образом, в каждой ячейке таблицы  T  будут стоять две цифры

буква	0	1	2	3
Н	11	12	15	17
П	00	23	33	33
К	00	04	06	08

Опишем смысл состояний и действий. Сначала состояния

0. Начальное состояние. Строка обязательно должна начинаться с буквы Н. В это состояние процесс возвращается из любого при появлении буквы К.
1. Прочтено начало группы. Из этого состояния можно перейти в состояние 2 при продолжении группы и в состояние 1 при новом начале.
2. Группа содержит два числа. Из этого состояния можно перейти в состояние 3 при продолжении группы и в состояние 1 при новом начале.
3. Группа содержит больше чем два числа. Переходы такие же, как в состоянии 2. Но действия, конечно, будут отличаться.

0. Операция Е0: Сообщение об ошибке "Неправильное начало строки".
1. Операция Е1: Запомнить в P1 номер начальной страницы.
2. Операция Е2: напечатать P1. Операция Е3: напечатать запятую и пробел. Операция Е1.
3. Операция Е4: запомнить в P2 номер конечной страницы группы.
4. Операция Е2. Операция Е5: напечатать точку.
5. Операция Е2. Операция Е3. Операция Е6: напечатать P2. Операция Е7: как Е3. Операция Е1.
6. Операция Е2. Операция Е3. Операция Е5.
7. Операция Е2. Операция Е8: напечатать тире. Операция Е6. Операция Е5.
8. Операция Е2. Операция Е8. Операция Е5.

Такое описание действий позволяет очень удобно программировать их выполнение в виде последовательности условных выражений:

    if IsFlag(0) then E0 fi;
    if IsFlag(2) then E2 fi;
    if IsFlag(3) then E3 fi;
    if IsFlag(8) then E8 fi;
    if IsFlag(5) then E5 fi;
    if IsFlag(6) then E6 fi;
    if IsFlag(7) then E3 fi;
    if IsFlag(4) then E4 fi;
    if IsFlag(1) then E1 fi;
Здесь предполагается, что каждому действию сопоставляется девятибитовый набор, в котором «выставлены» все операции, предусмотренные данным действием. Например, действию 5 сопоставляется набор (нумеруемый справа налево) 001001110, который можно представить целым числом 78. Функция IsFlag(k) вырабатывает логическое значение бит номер k выставлен. Пусть код вызываемого действия сохранен в переменной kAct. Получаем
  function IsFlag(int k): Boolean;
    int mask;
  begin
    mask := 1 << k;
    result := ( (kAct and mask) > 0 )
  end;

Пусть мы имеем некоторое дерево кодов Хаффмена. Напомню. что это двоичное дерево с  n  листьями и  n−1  узлами. Листьям соответствуют символы сжимавшегося текста, а из каждого узла выходят две дуги, соответствующие 0 и 1 в очередной позиции кодовой последовательности. Декодируя сжатый текст, мы читаем 0-1 последовательность и перемещаемся по кодовому дереву, начиная от корня. Когда процесс декодирования доходит до листа, то в результат записывается буква, соответствующая этому листу, а процесс возвращается в корень дерева.

Автомат уже и построен. В нем состояниями являются узлы кодового дерева, начальным состоянием — корень этого дерева, входной алфавит состоит из 0 и 1, выходной алфавит — из алфавита сжатого текста (в обычном использовании алгоритма Хаффмена выходным алфавмтом является набор всех возможных значений байта). Переход из каждого состояния происходит либо к прямым потомкам, либо (если потомок — это лист) к корню дерева. При переходе к корню вырабатывается буква выходного алфавита, а в остальных случаях «пустая буква» — ничего не вырабатывается.

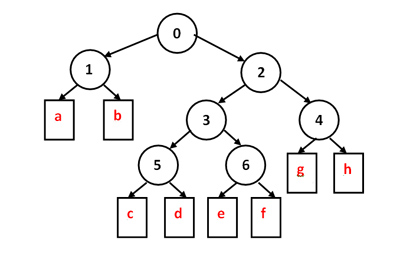
Вот небольшое кодовое дерево и соответствующий ему автомат, заданный таблицей.

буква   0    1    2    3    4    5    6  0  1   a   3   5   g   c   e  1  2   b   4   6   h   d   f  В клетках матрицы записаны либо номера состояний, в которые процесс переходит из данного, либо вырабатываемые буквы — в случае, когда процесс переходит в состояние 0.

Схема декодирования получилась настолько простой, что ее можно при необходимости и усложнить. Например, в некоторых случаях рисунок, сделанный с использованием небольшого количества цветов, можно сжато записать, кодируя каждую строчку последовательностью пар чисел (номер цвета, число пискелей). При сжатии такой записи правильно вырабатывать код Хаффмена отдельно для цветов и длин монохромных отрезков. Соответствующие цепочки можно потом писать по-очереди, а при декодировании строить автомат из двух деревьев, переходя от листа одного дерева к корню другого.

С аналогичными расписаниями, в гораздо более сложных ситуациях, приходится сталкиваться почти повсеместно: в строительстве: в качестве важнейшего практического усложнения модели сетевого планирования, в промышленности: при определении планов производства с учетом сроков выпуска изделий и возможностей используемого оборудования.

В теории расписаний используется много приближенных методов с разными базовыми идеями, одна из которых красочно называется «моделирование логики диспетчера».