Пусть задан граф <M,N>, в котором выделены две вершины,  iB  и  iE. Будем предполагать, что в этом графе нет контуров и что любая дуга лежит на каком-нибудь пути из  iB  в  iE. Пусть каждой дуге  j О N   сопоставлено неотрицательное число время выполнения этой дуги.  t[j]. Временем выполнения пути будет называться сумма времен дуг, входящих в этот путь. Требуется найти путь с наибольшим временем выполнения.

Для решения этой задачи можно использовать метод, похожий на метод Дейкстры. Мы определяем и пересчитываем вектор
 τ[M] максимальных времен выполнения путей до каждой вершины. Естественно, что начальные значения должны приниматься нулевыми, а значение в вершине пересчитывается, если предложено значение выше имеющегося. Более существенно отличие от метода Дейкстры в способе, которым выбирается вершина, переводимая из множества  M1  в множество  M0. Именно, считаются вычисленными расстояния до тех вершин, для которых просмотрены все входящие в них дуги.

Первоначально множество M0 пусто, M1 состоит из начальной вершины со значением τ=0, остальные вершины находятся в M2.

В подготовку вычислений входит вычисление количества дуг, входящих в каждую вершину. Для хранения этих данных мы используем массив Count[M], который заполняется двумя простыми циклами. Именно эти счетчики используются при решении, какие вершины нужно переводить в множество M1

  for i in M do Count[i] := 0 od;
  for j in N do Count[iEnd[j]] +:= 1 od;

Вычислительный процесс представляет собой цикл, который продолжается до тех пор, пока не исчерпается множество M1 (на каждой итерации из него одна вершина убирается, но множество может и пополняться), либо пока требуемая нам вершина не попадет в множество M0.

  bContinue := TRUE;
  while bContinue do
    GET_AND_TREATE_A_VERTEX;
    bContinue := IS_NONEMPTY_M1;
  od;

Выбор вершины в множестве M1 здесь очень прост.

GET_AND_TREATE_A_VERTEX ≡
  i0 := FIRST_VERTEX_IN_M1;
  MOVE_FROM_M1_TO_M0(i0);
  SCAN_ARCS_EXITING_FROM(i0);

Берется первая вершина в цепном списке и переводится в множество M0 — это просто. Выполняется цикл просмотра дуг, выходящих из вершины i0.

SCAN_ARCS_EXITING_FROM(i0) ≡
  for j in EXIT_ARCS(i0) do
    TREATE_ARC(j)
  od;

Обработка дуг несколько отличается от того, что было раньше.

TREATE_ARC(j) ≡
  iE := iEnd(j); τ1 := τ[i0]+w[j]; Count[iE] -:= 1;
  if τ[iE] < τ1 then UPDATE(iE,τ1,j) fi;
  if Count[iE] = 0 then MOVE_FROM_M2_TO_M1(iE) fi;

Поясним, что здесь делается. Получив номер дуги j, мы фиксируем ее параметры и уменьшаем на единицу счетчик конца дуги. Если нужно, увеличиваем значение . Если у вершины iE обработаны все дуги, переводим ее в множество M1. Элементы этого множества могут обрабатываться в любом порядке, и нам проще всего устроить цепной список со стековой дисциплиной.

Алгоритм очень простой. Можно было бы вести вычисления, начиная не с начальной вершины графа, а с конечной. Сейчас мы посмотрим. где применяется эта задача.

В начале XX века в Соединенных Штатах Америки появился интерес к научной организации труда, направлению, которое связывается с именем американского инженера Фредерика Тейлора. Одним из сторонников Тейлора был изображенный на снимке слева Генри Гант (1861—1919). он предложил простое и эффективное средство визуализации расписаний, известное как ленточная диаграмма.

В случаях, когда требуется аналозировать совместную работу нескольких исполнителей над отдельными заданиями, Гант предложил изображать периоды занятости исполнителей 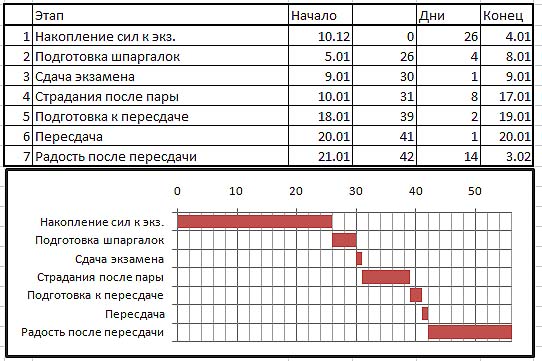задачами на календарных осях. Здесь каждому исполнителю соответствует своя гори­зонтальная лента, а каждое задание занимает на этих осях отрезки, соответствующие запланированным периодам, когда данный исполнитель должен выполнять данное задание.

Пример такой диаграммы я сделал по мотивам книги Б.Ю.Левита «Диаграммы Excel в экономических моделях». Как видите, ленточные диаграммы Ганта популярны до сих пор. К сожалению, моя диаграмма оказалось не так красива, как у автора.

В середине XX века проектные разработки чудовищно усложнились, и диаграммы Ганта утратили для них свою наглядность. Следующим шагом в визуализации контроля над сложными работами стало использование техники графов.

В этом подходе особое внимание уделялось взамным зависимостям выполняемых работ. Эти зависимости (не очень хорошо просматриваемые в ленточных диаграммах) влияют на последовательность выполнения работ и определяют общую продолжительность выполнения проекта.

Было создано много вариантов такой системы, наиболее известные названия — это Система PERT (Program Evaluation and Review Technique), а также CPM (Critical Path Method).

Критическим путем в этих методах сетевого планирования называется путь наибольшей продолжительности, идущий от начала и до конца проекта. Именно здесь и появляется задача, о которой шла речь в начале лекции.

Сейчас мы обсудим некоторые аспекты построения сетевого графика — графа, в котором ищется этот критический путь.

Легко привести пример: Стена в квартире должна быть оштукатурена до того, как она будет покрашена.

В термин отношение предшествования естественно входит условие его транзитивности: стена должна быть поставлена до того, как будет оштукатурена, и, следовательно, до ее окраски.

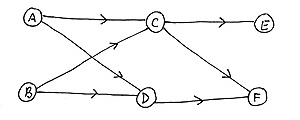Казалось бы, мы можем прямо строить граф <M,N>, в котором вершинами будут работы, а дугами попарные связи предшествования работ.

Смотрите, как все хорошо видно. У нас есть шесть работ, они разбиты на три этапа. Работы A и B предшествуют работам C и D, которые в свою очередь предшествуют работе F, работа E имеет свою особенность, ей предшествует только работа C.

Но далеко не всегда то, что хорошо на маленьком учебном примере, оказывается удобным в реальном применении. Рассмотрим еще один пример.

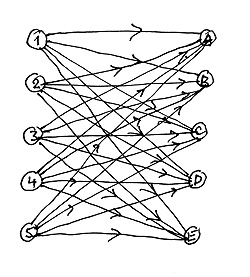
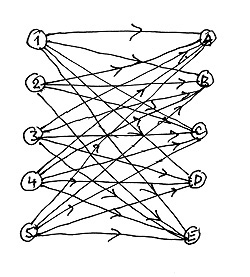Новый пример совсем ненамного больше предыдущего. А этапов в нем даже меньше — всего два. Все работы разбиты на два этапа, и каждая работа первого этапа предшествует каждой работе второго. Но, посмотрите на правый рисунок. В нем на одну дугу меньше, дугу из вершины 2 в вершину D я специально убрал. Контролировать правильность такого рисунка стало труднее.

В реальных условиях трудности возрастают неизмеримо. Поэтому в модели проекта, принятой в сетевых графиках используется схема, в которой работы представляются дугами. Естественно возникает вопрос, чему в этой модели соответствуют вершины.

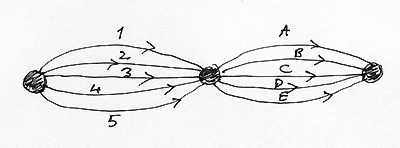На рисунке слева изображена модель той же зависимости между 10 работами. Как видите, все выглядит гораздо привлекательнее. Вершинами этого графа являются начала и концы этапов. Появилось общее начало и общее завершение.

Что же делать, если первоначально мы никаких этапов не ввели и ввести не могли? Стандартные руководства по сетевому планирова­нию описывают вершины графа как события, которые беспомощно определяются как «начала и концы работ». Рекомендуется просто строить граф, вводя события по мере надобности.

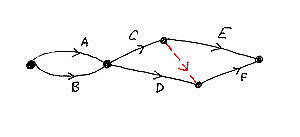При этом в случаях, когда из-за сложных зависимостей построить граф не удается, рекомендуется вводить дополнительные дуги которые соответствуют фиктивным работам (dummy jobs).

На рисунке справа вы видите граф «работы-дуги», построенный для первого, самого простого, примера. В нем, при всей его простоте, там понадобилась фиктивная работа, которая изображена на картинке красным пунктиром.

Сейчас мы рассмотрим принципиальный способ построения сетевого графика, в котором одновременно получаются и вершины графа и необходимые фиктивные дуги. Нужно предупредить, что эта модель слишком громоздка для практического применения — есть программы, которые строят (неизвестно что!) гораздо проще.

Составители множеств  P(j)  не в силах предусмотреть всех предшественников своих работ, они четко должны видеть непосредственных предшественников, но иногда могут включать в список и более далекие работы. Для унификации этих данных их нужно транзитивно замкнуть — здесь этот термин вполне применим, так как строится отношение на множестве  J. Обозначим через  PT(j)  транзитивно замкнутое множество предшественников работы  j.

Эти множества очень важны, они определяют для каждой работы условия начала ее выполнения. Значит, работы с одинаковыми множествами предшествования должны изображаться дугами, начинающимися в одной и той же вершине. Таким образом, среди множеств  PT(j)  нам следует выбрать различные и как-то их проиндексировать. Получится некоторое множество индексов  K

Полезно привести маленький пример. Рассмотрим приведенную выше модель с шестью работами. В ней J =  { A,B,C,D,E,F }. Очевидно, что множества  P(A)  и  P(B)  пусты,  P(C) = P(D) =  { A,B }, выберем  P(E) =  { C },  P(F) = P() =  { A,C,D }. При транзитивном замыкании получаем  PT(A)  и  PT(B)  пусты,  PT(C) = PT(D) =  { A,B },  PT(E) =  { A,B,C },  PT(F) =  {A,B,C,D }. Таким образом, у нас получилось четыре разных множества предшествующих работ. Обозначим их через  bA,  bC,  bE,  bF.

Что же касается концов дуг, то они должны быть одинаковы у работ, одинаково влияющих на другие работы. Например, таковы работы  A и  B, а также  E и  F, которые ни на что не влияют.

Обозначим эти множества через  eA,  eC,  eD,  eE.

В общем случае эти множества получаются как части разбиения, являющегося произведением разбиений, соответствующих множествам  PT(j) и их дополнениям до  J.

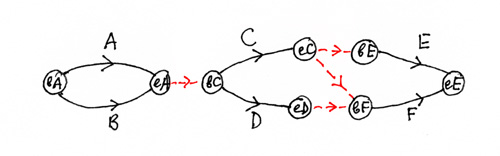Теперь на нашем примере пора посмотреть, как собирается наш граф и чего нам еще недостает.

Нарисовав в виде дуг все работы и их начала и концы, мы видим, что граф у нас «не собрался» и нужна еще какая-то информация. Замечаем, что у нас совпадают множества работ, обозначенные как  eA  и  bC, а также  eC  и  bE. Что же касается множества  bF, то оно является объединением  eC  и  eD. Чтобы показать зависимость каждой работы от предшествующих работ, мы должны подвести эти работы (прямо или косвенно) к началу данной работы. Проведем (красным пунктиром) линии, «составляющие» множества  b...  из множеств  e.... Получится черновой вариант сетевого графика — такой граф строится всегда. Теперь нам достаточно убрать дополнительные дуги там, где без них можно обойтись. Получится граф, изображенный ранее.

Однако, на этом работа с сетевым графиком не кончается. Каждой работе  j, входящей в график сопоставляется время  t[j], необходимое для выполнения этой работы. Разумеется, указать это время точно невозможно, используются оценки (замечу, что специалисты считают это время случайным и часто используют так называемое бета-распределение (мы такого распределения не проходили!). Но полезна и приблизительная оценка.

По найденным оценкам строится критический путь от начального события до завершающего события. Более того, находятся все дуги, входящие в критические пути и в пути, продолжительность которых близка к максимальной. Эти работы становятся объектом пристального внимания администрации проекта.

Прежде всего, по такому расчету видно, укладывается ли выполнение проекта в намеченный срок. Если нет, то может потребоваться изменение последовательности работ и смена технологии в некоторых частях проекта.

Когда график исполнения проекта составлен окончательно, все время идет «мониторинг» этого исполнения — вносятся данные о реальных временах исполнения отдельных работ, об изменении технологических зависимостей и т. д., и критические пути постоянно пересчитываются, что совсем не сложно.

Нужно иметь в виду, что сама сетевая модель слишком проста, обычно она усложняется многими факторами, среди которых самый важный — это ограниченность технических средств, из-за которой не все запланированные работы могут выполняться одновременно.

Поэтому сетевые графики включаются сейчас в гораздо более сложные компьютерные системы управления процессами, где они сочетаются с методами так называемых теории расписаний и теории управления запасами.

Справа вы видите обложку совсем новой книги К. Четфилда и Д. Джонсона «Microsoft Office Project 2007. Шаг за шагом», ЭКОМ Паблишерз, 2007. Это учебник, выпущенный для фирменных курсов, на которых изучается известный программный продукт. Другая крайность. Вас учат нажимать кнопки, в частности, при построении упоминавшейся нами диаграммы Ганта и сетевого графика, но что это такое вам здесь не объяснят.