Такое дерево будет называться минимальным остовным деревом.

Мы рассмотрим два метода. Первый из них использует с некоторым усовершенствованием конструкцию постепенного расширения поддерева дугами, выбираемыми из границы (как это делелось при доказательстве теоремы об остовном дереве). Второй алгоритм работает по-другому.

Предложенный ими алгоритм очень прост, для его описания хватит пары строк:

Дерево строится так, как описано в доказательстве теоремы об остовном дереве, но на каждом шаге для пополнения дерева из границы выбирается дуга с наименьшим весом.

Теорема. Остовное дерево, которое строится описанным алгоритмом, имеет минимальный вес. Доказательство. Пусть N* — множество дуг рассматриваемого дерева. Нам понадобится нумерация этих дуг, о которой говорилось в теореме об остовном дереве. Возьмем какое-либо другое остовное дерево <M,N'>. Докажем, что вес этого дерева не меньше N*. Для этого покажем, что если множества N' и N* не совпадают, то можно построить дерево <M,N''>, вес которого будет не больше, чем вес N', а множество N'' будет больше похоже на N*, чем множество N'. Вся соль в подходящем определении этих слов. Как измерять сходство множеств дуг? Оно измеряется очень специфически. Рассмотрим разность N*\N'. Это множество состоит из нумерованных дуг, не входящих в N'. Выберем среди них дугу с наименьшим номером. Именно этот номер и будем считать мерой сходства N' и N* — чем он больше, тем сходство больше. Обозначим этот номер через k, а дугу с этим номером через jk. Покажем, что можно получить требуемое улучшение N', заменив в нем одну дугу на jk. Добавим дугу jk в граф <M,N'> и рассмотрим единственный образовавшийся там цикл. Этот цикл состоит из дуги jk и цепи, соединяющей начало и конец jk. Один конец цепи имеет в нашей нумерации номер k, а другой — меньше чем k. Легко видеть, что в цепи есть две соседние вершины, у одной из которых номер меньше k, а у другой не меньше k. Их соединяет какая-то дуга jl. Очевидно, что на k-й итерации нашего алгоритма эта дуга принадлежала границе, и по выбору jk ее вес не превосходит веса jk — минимального для данной границы. Теперь ясно, что замена дуги jl на дугу jk даст множество дуг с весом, не большим чем раньше и более похожим на N*. Это улучшение множества N' можно повторять до тех пор, пока оно не совпадет с множеством N*, и вес при каждом улучшении будет разве лишь убывать. Теорема доказана.

На этих шести рисунках показаны исходный граф, несколько итераций метода и окончательное решение.

На рисунках, соответствующих итерациям черным показано частичное дерево, розовым цветом граница, а красным — лучшая дуга границы и добавляемая вершина. Голубоватым нарисованы дуги, соединяющие вершины дерева и в дерево не входящие.

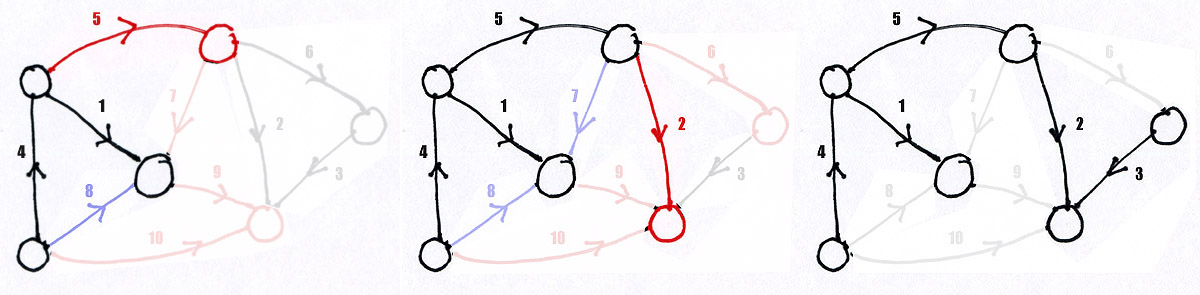
В этом примере не видно трудностей, связанных с перестройкой границы на каждой итерации. Для преодоления этих трудностей предпринимались специальные модификации метода.

Алгоритм состоит из двух фаз. На подготовительной фазе все дуги удаляются из дерева и упорядочиваются по возрастанию их весов. В графе остаются только вершины, каждая из которых образует отдельную компоненту связности.

Во второй фазе дуги перебираются в порядке возрастания веса. Если начало и конец очередной дуги принадлежат одной и той же компоненте связности, дуга игнорируется. Если же они лежат в разных компонентах связности. дуга добавляется к графу, а эти две компоненты связности объединяются в одну. Если число компонент связности дойдет до 1, цикл завершается досрочно.

Алгоритм Краскала мы рассмотрим на том же графе. Начинаем с графа, в котором все дуги удалены, каждая вершина — отдельная компонента связности.

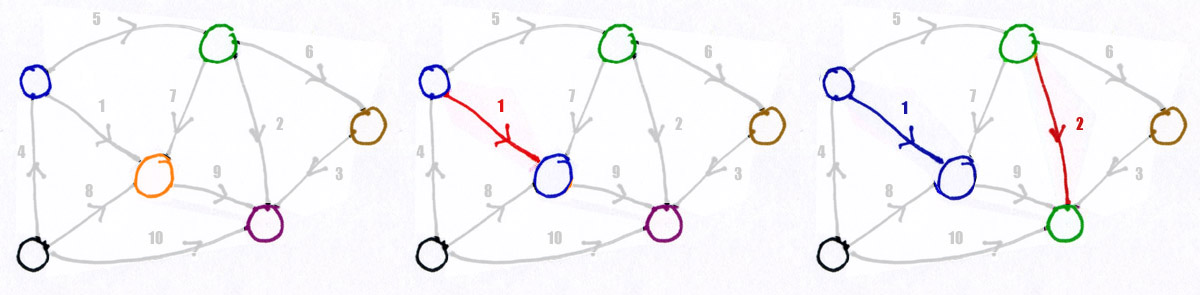
Первая дуга соединяет две различные компоненты связности, они объединяются в одну. То же происходит и со второй дугой. Третья и четвертая дуги также включаются в граф, который становится связным, и остальные дуги даже не рассматриваются.

В этом примере нам ни разу не встретился случай, когда очередную дугу следует пропустить, так как она совединяет две вершины из одной компоненты связности. Представьте себе, что после дуги 2 нам попалась бы дуга 6. Мы бы ее просто игнорировали.

Фактически алгоритм состоит из двух фаз, трудоемкости которых нужно считать отдельно.

Первая фаза — это упорядочение дуг по возрастанию веса. Ее трудоемкость — это трудоемкость обычной сотрировки, но в конкретных задачах она может быть меньше, иногда дуги могут быть уже упорядочены.

Вторая фаза — это цикл, в котором просматриваются упорядочнные дуги, и мы пытаемся включить эти дуги в создаваемое дерево. Трудоемкость выполнения тела цикла зависит от того, как организована информация о компонентах связности имеющегося графа. Проверку совпадения компонент лекго сделать константной. Но примерно m = | M | компонент будут трудными: потребуется включать дугу в дерево и перестраивать информацию о компонентах. Описание алгоритма перестройки можно найти в моей книжке.

Ярник был не первым. В 1926 г. Интересный метод предложил чешский математик Отакар Борувка (1899-1995).

Полезный обзор Глеба Рыбакова опубликован на сайте ИФМО в 2005 г.