Прием-2001. Задачи, предложенные абитуриентам на вступительных экзаменах по математике
Математико-механический, прикладной математики-процессов управления ф-ты
СПбГУ, дневное отделение.
Первый вариант
-
Косцы должны выкосить два луга. Начав косить больший луг, через 2 часа работы они разделились:
часть осталась на первом лугу, а другая (большая) часть пошла косить второй луг, площадью вдвое меньше первого,
и закончила работу одновременно с первой группой. Требуется определить, сколько косцов осталось работать на
большем лугу, если известно, что один косец скашивает малый луг за 3 дня работы по 8 часов.
-
Решить уравнение

-
Решить неравенство
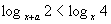
при условии, что 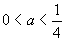
-
В треугольнике ABC известны стороны: AB = 5, BC = 8, AC = 7.
На биссектрисе угла A (внутри треугольника ABC) выбрана точка O так,
что площади треугольников AOB, AOC, BOC, взятые в указанном порядке, образуют арифметическую прогрессию. Найти эту прогрессию.
-
Найти объем треугольной пирамиды, каждая грань которой представляет собой треугольник со сторонами длиной
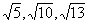 .
.
Второй вариант
-
Две бригады маляров красят два цеха. После 3 часов совместной работы в первом цехе вторая бригада перешла во второй цех,
объем работы в котором вдвое меньше, чем в первом. Требуется определить, сколько маляров было во второй бригаде, если известно,
что покраска обоих цехов была закончена одновременно, а один маляр может покрасить меньший цех за 6 дней, работая по 8 часов.
-
Решить уравнение
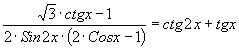
-
Решить неравенство
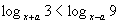
при условии, что 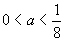
-
В треугольнике ABC известны стороны: AB = 5, BC = 8, AC = 7.
На биссектрисе угла A (внутри треугольника ABC) выбрана точка O так,
что площади треугольников AOB, BOC, AOC, взятые в указанном порядке, образуют арифметическую прогрессию. Найти эту прогрессию.
-
Найти объем треугольной пирамиды, каждая грань которой представляет собой треугольник со сторонами длиной
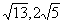 и 5.
и 5.
Ответы на задачи