| (1) |
Приведем, следуя Г. Шустеру [3], краткий обзор определений, результатов и методов нелинейной механики, используемых далее при анализе предельного поведения итерационных схем.
Пусть мы имеем уравнение
| (1) |
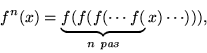
Пусть ![]() -- неподвижные точки уравнения
-- неподвижные точки уравнения ![]() . Они образуют предельный цикл периода
. Они образуют предельный цикл периода ![]() , если мультипликатор
, если мультипликатор
![]() по модулю меньше единицы:
по модулю меньше единицы:
| (2) |
Если ![]() отображает некоторый отрезок
отображает некоторый отрезок ![]() в себя и имеет нанем единственный максимум, причем
в себя и имеет нанем единственный максимум, причем ![]() по обе стороны максимума монотонна(унимодальна), то у динамической
системы
по обе стороны максимума монотонна(унимодальна), то у динамической
системы ![]() может появиться свойство самоподобия -- каскад бифуркаций Фейгенбаума. Именно,
если
может появиться свойство самоподобия -- каскад бифуркаций Фейгенбаума. Именно,
если ![]() зависит от некоторого параметра
зависит от некоторого параметра ![]() :
:![]() , -- то может существовать бесконечная последовательность значений параметра
, -- то может существовать бесконечная последовательность значений параметра
![]() (упорядоченная по возрастанию или убыванию
(упорядоченная по возрастанию или убыванию ![]() ):
):![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , -- такая, что в интервалах
, -- такая, что в интервалах![]() динамическая система
динамическая система ![]() имеет предельный цикл периода
имеет предельный цикл периода ![]() ипри этом последовательность
ипри этом последовательность ![]() имеет точку сгущения
имеет точку сгущения ![]() , определяемую соотношением
, определяемую соотношением
| (3) |
| (4) |
При ![]() динамическая система может иметь хаотический аттрактор, когда независимо от
начального значения
динамическая система может иметь хаотический аттрактор, когда независимо от
начального значения ![]() (при
(при ![]() ) предельное (при
) предельное (при![]() ) положение точки
) положение точки ![]() мы можем указать только с вероятностью
мы можем указать только с вероятностью
![]() попадания ее в интервал
попадания ее в интервал ![]() . Если
. Если ![]() не зависит от числа итераций
не зависит от числа итераций ![]() , то функция
, то функция ![]() называется плотностью инвариантной меры.
называется плотностью инвариантной меры.
Переход к хаосу через каскад удвоения периода называется мягкимпереходом .
При других значениях ![]() картина может быть еще сложнее.
картина может быть еще сложнее.
Хаусдорфова размерность ![]() хаотического аттрактора, какправило, не является целым числом. Она определяется
по формуле
хаотического аттрактора, какправило, не является целым числом. Она определяется
по формуле
| (5) |
Как пишет Г. Шустер [3], "настоящая первопричина нерегулярности определяется
свойством нелинейных систем экспоненциально быстро разводить первоначально
близкие траектории в ограниченной области фазового пространства", так что
"становится практически невозможно предсказать длительное поведение таких систем,
поскольку реально начальные условия можно задать лишь с конечной точностью,
а ошибки экспоненциально возрастают." Степень экспоненциального разбегания
характеризуется показателем Ляпунова ![]() , вычисляемым по формуле
, вычисляемым по формуле
Так как по правилу дифференцирования суперпозиции двух функций
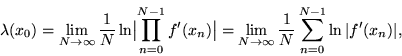 |
(6) |
Положительность показателя Ляпунова сигнализирует о наличии хаотической компоненты в аттракторе.
Отметим также теорему Шарковского [4]. Упорядочим натуральные числа следующим
образом:
| (7) | |||
Остановимся на процедуре вычисления плотности инвариантной меры. За одну
итерацию точка ![]() переходит в
переходит в ![]() , и поэтому любая функция
, и поэтому любая функция ![]() за одну итерацию переходит в функцию (напоминаем, что мы ограничились отрезком
за одну итерацию переходит в функцию (напоминаем, что мы ограничились отрезком
![]() как интервалом изменения переменной и функции)
как интервалом изменения переменной и функции)
| (8) |
![\begin{displaymath}\int _a^bF(x)\,\delta (x-y)\,dx=\cases {F(y)\quad
{\textit{пр...
...\quad y=a, y=b,\cr
0\quad \textit{при}\quad y\notin [a,b].\cr}
\end{displaymath}](img85.gif) |
(9) |
Так как, по определению, плотность инвариантной меры ![]() при итерациине меняется, то при
при итерациине меняется, то при ![]() в (8) имеем
в (8) имеем
| (10) |
Таким образом, ![]() удовлетворяет уравнению (10), которое называется уравнением Фробениуса - Перрона.
В главе 8 мы вернемся к выводу этого уравнения и покажем, что итерационную
схему (1) можно рассматривать как стационарный марковский процесс с дискретным
временем и плотностью вероятности перехода
удовлетворяет уравнению (10), которое называется уравнением Фробениуса - Перрона.
В главе 8 мы вернемся к выводу этого уравнения и покажем, что итерационную
схему (1) можно рассматривать как стационарный марковский процесс с дискретным
временем и плотностью вероятности перехода
![]() (простейший детерминированный марковский процесс).
(простейший детерминированный марковский процесс).
Естественно считать плотность ![]() не существующей, если
не существующей, если ![]() во всем интервале изменения
во всем интервале изменения ![]() (т.е. в
(т.е. в ![]() ).
).
Рассмотрим примеры решения уравнения Фробениуса - Перрона.
П р и м е р 1. Ответим на вопрос, существует ли плотность инвариантной
меры для линейной функции ![]() , т.е. когда
, т.е. когда
| (11) |
В соответствии с определением (9) ![]() -функции уравнение (10) дл
-функции уравнение (10) дл![]() в виде (11) превращается в функциональное уравнение
в виде (11) превращается в функциональное уравнение
| (12) |
| (13) |
Ищем решение уравнения (13) в классе непрерывных функций, полезных возможностью
переходить к пределу под знаком функции. Воспользуемся методом последовательных
подстановок [5, с.31-33]. Именно, положим в (13) ![]() и переобозначим после этого
и переобозначим после этого ![]() через
через ![]() . Мы получаем
. Мы получаем
| (14) |
| (15) |
Аналогичным образом, заменив в (14) снова ![]() на
на ![]() и подставив результат в (15), находим
и подставив результат в (15), находим
Продолжая процесс далее, на ![]() -ом шаге получаем
-ом шаге получаем
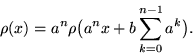 |
(16) |
Переходя к пределу в (16) при ![]() , убеждаемся в том, что
, убеждаемся в том, что![]() при
при ![]() для всех
для всех ![]() , т.е. плотность инвариантной меры не существует. В случае
, т.е. плотность инвариантной меры не существует. В случае ![]() в силу (11) обязательно
в силу (11) обязательно ![]() , так что
, так что ![]() ,но это тождественное преобразование отрезка
,но это тождественное преобразование отрезка ![]() в себя не интересно.
в себя не интересно.
Итак, линейное преобразование не имеет плотности инвариантной меры (оно при итерировании и не хаотизируется).
П р и м е р 2. Рассмотрим так называемое треугольное преобразование
отрезка ![]() в себя:
в себя:
| (17) |
| (18) |
Ищем его решение в виде ряда по степеням ![]() :
:
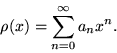 |
(19) |
Подставив (19) в (18), получаем
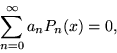 |
(20) |
| (21) |
В случае ![]() видим, что в (21)
видим, что в (21) ![]() , и поэтому
, и поэтому ![]() может быть произвольной константой. Все прочие
может быть произвольной константой. Все прочие ![]() образуют чебышевскую систему, так что равенство (20) для произвольных
образуют чебышевскую систему, так что равенство (20) для произвольных ![]() возможно только при
возможно только при![]() ,
, ![]() . Таким образом, для треугольного преобразования плотность инвариантной меры
. Таким образом, для треугольного преобразования плотность инвариантной меры
![]() существует только при
существует только при ![]() и равна константе
и равна константе ![]() , которую выбираем из условия нормировки:
, которую выбираем из условия нормировки:
| (22) |
П р и м е р 3. Покажем теперь, что плотность инвариантной меры может отличаться
от константы. Рассмотрим логистическое отображение отрезка ![]() в себя:
в себя:
| (23) |
Оно введено в 1845 г. П. Ф. Ферхюльстом для описания динамики популяции
взамкнутой среде. Здесь ![]() -- численность особей в рассматриваемый год, которая пропорциональна численности
особей
-- численность особей в рассматриваемый год, которая пропорциональна численности
особей ![]() в предыдущий год и свободной части
в предыдущий год и свободной части ![]() жизненного пространства. Параметр
жизненного пространства. Параметр ![]() зависит от плодовитости, жизненных ресурсов и т.д. [3].
зависит от плодовитости, жизненных ресурсов и т.д. [3].
Это же отображение описывает ситуацию с ценообразованием на замкнутом рынке,где
![]() -- цена всех продаж в день, пропорциональная цене всех продаж за предыдущий
день и сумме денег
-- цена всех продаж в день, пропорциональная цене всех продаж за предыдущий
день и сумме денег ![]() , оставшихся у покупателей накануне (за единицу принята вся совокупность денег,
могущая быть истраченной на рынке).
, оставшихся у покупателей накануне (за единицу принята вся совокупность денег,
могущая быть истраченной на рынке).
Чтобы ![]() , параметр
, параметр ![]() в (23) должен удовлетворять условию
в (23) должен удовлетворять условию
| (24) |
Итерационная схема (1) с функцией (23) изучена хорошо. При ![]() она демонстрирует мягкий переход к хаосу в случае увеличения
она демонстрирует мягкий переход к хаосу в случае увеличения ![]() до некоторой точки сгущения
до некоторой точки сгущения ![]() [3].
[3].
Уравнение Фробениуса - Перрона (10) для функции (23) имеет вид
| (25) |
| (26) |
Вещественное значение обратной к (23) функции (25) во всем интервале ![]() существует только при
существует только при ![]() . Этой величиной
. Этой величиной ![]() и ограничимся. Полагая в(25)-(26)
и ограничимся. Полагая в(25)-(26) ![]() и заменяя
и заменяя ![]() в (25) на правую часть (26), получаем
в (25) на правую часть (26), получаем
Используя определение (9) ![]() -функции, находим отсюда функциональное уравнение
-функции, находим отсюда функциональное уравнение
| (27) |
Если сделать в (27) замену ![]() , то получим уравнение
, то получим уравнение
| (28) |
Уравнения (27)-(28) показывают, что в точках ![]() и
и ![]() функция
функция ![]() может обращаться в бесконечность (если
может обращаться в бесконечность (если
![]() ). Поэтому ищем решение в (27) в виде
). Поэтому ищем решение в (27) в виде
![\begin{displaymath}\rho (y)=\frac{1}{2\sqrt{y(1-y)}}
\sum _{n=0}^{\infty }a_n[4y(1-y)]^n.\end{displaymath}](img135.gif) |
(29) |
Так как
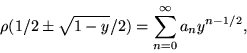
![\begin{displaymath}\sum _{n=1}^{\infty}a_n\{[4y(1-y)]^n-y^n\}=0
\end{displaymath}](img137.gif) |
(30) |
З а м е ч а н и е. Итерационные схемы типа (1) лежат в основе вычислительной математики. Поэтому обнаружение хаотических аттракторов у самых простых нелинейных отображений ограничивает сферу применимости вычислительных методов.
Возьмем, к примеру, одну из простейших вычислительных процедур -- отыскание
вещественных корней функции действительного переменного![]() по методу Ньютона:
по методу Ньютона:
| (31) |
| (32) |
О хаотизации других вычислительных процедур расскажем в конце § 3.